浅析Dijkstra单源最短路径算法
- 2020-10-27 09:45:08
- 算法 原创
- 5017
单源最短路径问题
给定 加权有向图G=(V,E,W),每条边的权值w为 非负数,表示两个顶点间的距离。源点s∈V。
求:从s出发到其他各个顶点的最短路径。
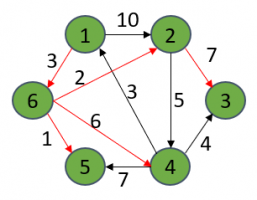
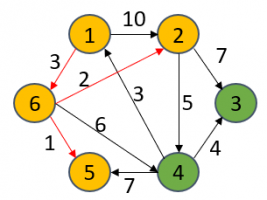
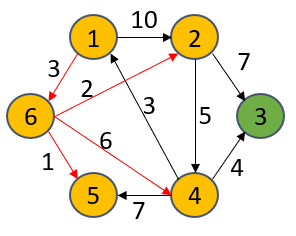
如上图所示,以1为源点,计算到其余各个顶点的最短距离(我已用红线标出)。下面列出了最终解:
源点:1
1->6->2 : short[2] = 5
1->6->2->3 : short[3] = 12
1->6->4 : short[4] = 9
1->6->5 : short[5] = 4
1->6v : short[6] = 3
Dijkstra算法相关概念
S集合:当从s到x(x ∈V )的最短路径找到时,则x ∈S。当所有顶点都进入S集合时,算法结束。初始:S={s},当S=V时算法结束。
从s到u相对于S的最短路径:指从s到u且仅经过S中顶点的最短路径。
dist[u]:从s到u相对于S的最短路径长度
short[u]:从s到u最短路径的长度(算法最终解)
dist[u] ≥ short[u]
Dijkstra算法采用贪心算法模式,算法过程就是通过计算dist[u],不断扩充S集合,同时dist[u]会不断优化改善,直到dist[u] = short[u],并将其放到S中,当所有顶点都放入S集合时,算法结束。
算法设计思想
输入:加权有向图G=(V,E,W)V={1,2,…,n}, s=1
输出:从s到每个顶点的最短路径
- 初始S={1}
- 对于u ∈V-S,计算1到u的相对于S的最短路,长度为dist[u]
- 选择V-S中dist值最小的那个顶点,加入S。
- 继续上述过程,直到S=V为止。
实例
输入:G=(V,E,W),源点1V={1,2,3,4,5,6}
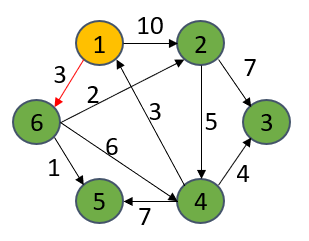
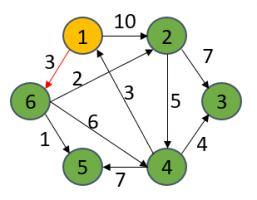
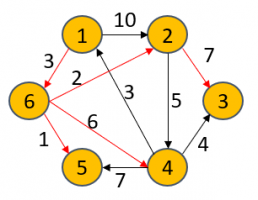
初始S集合只有1,计算直接从1能到达的顶点的距离,其他不能从1号顶点直接到达的顶点都记为无穷大。此时从dist[u]里找出最短距离的顶点(6号),并将其放进S集合。
S={1}
dist[1] = 0
dist[2] = 10
dist[6 ] = 3
dist[3] = ∞
dist[4] = ∞
dist[5] = ∞
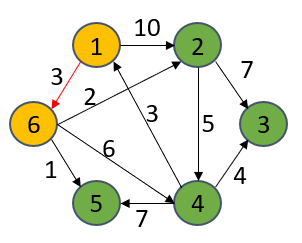
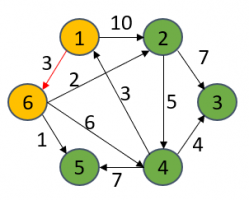
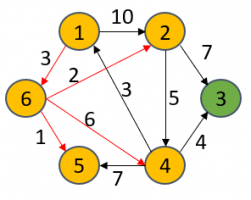
当把6号顶点放进S集合后,经由6号顶点出发到达的顶点的最短距离可能会被优化更新,因为该算法的思想很“贪心”,谁更短我要谁!比如1->6->2要比1->2距离更短,所以dist[2]被更新为5,从专业术语上讲,这个“更新”过程叫做松弛,其他点同理。然后从dist[u]里找出最短的路径的那个顶点(5号),并放进S集合里。
S={1,6}
dist[1] = 0
dist[6] = 3
dist[2] = 5
dist[4] = 9
dist[5] = 4
dist[3] = ∞
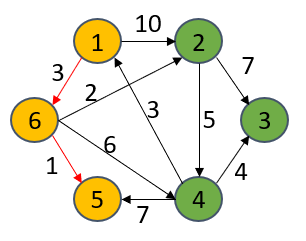
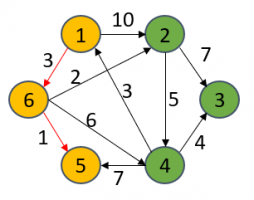
后面的操作步骤其实就是重复上面的操作。即当S集合里有个新的顶点后,就可能会更新其他点的最短距离,更新一遍后,找出当前最短距离的dist[u],并将该顶点放进S集合。后面不重复阐述。
S={1,6,5}
dist[1] = 0
dist[6] = 3
dist[5] = 4
dist[2] = 5
dist[4] = 9
dist[3] = ∞
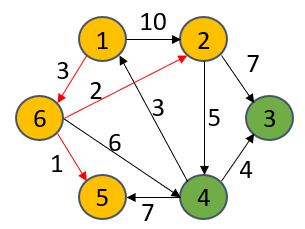
S={1,6,5,2}
dist[1] = 0
dist[6] = 3
dist[5] = 4
dist[2] = 5
dist[4] = 9
dist[3] = 12
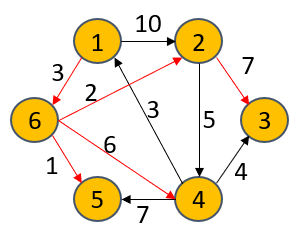
S={1,6,5,2,4}
dist[1] = 0
dist[6] = 3
dist[5] = 4
dist[2] = 5
dist[4] = 9
dist[3] = 12
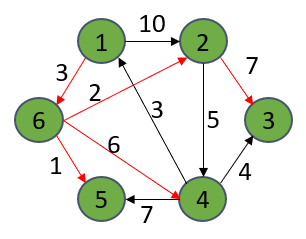
S={1,6,5,2,4,3}
dist[1] = 0
dist[6] = 3
dist[5] = 4
dist[2] = 5
dist[4] = 9
dist[3] = 12
当有向图中的所有顶点都进入了S集合后,算法结束,此时的dist[u]的值其实就是最初我们找出的那个最终解short[u],所以,算法结束时,dist[u]=short[u],得到最终解。
文章分类